Implementation of Hash Table in Python using Separate Chaining
A hash table is a data structure that allows for quick insertion, deletion, and retrieval of data. It works by using a hash function to map a key to an index in an array. In this article, we will implement a hash table in Python using separate chaining to handle collisions.
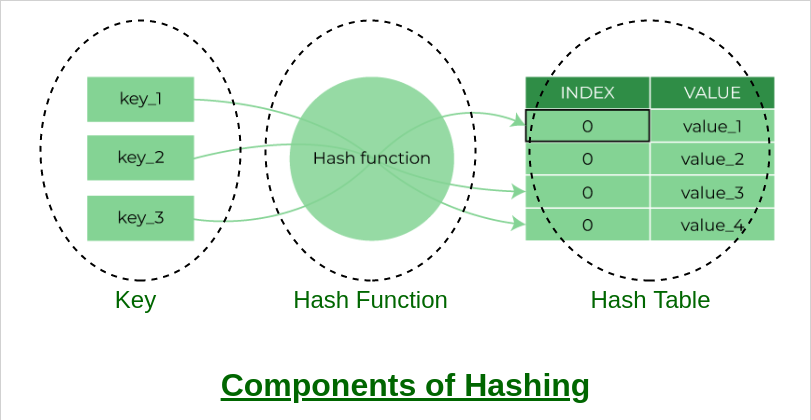
Components of hashing
Separate chaining is a technique used to handle collisions in a hash table. When two or more keys map to the same index in the array, we store them in a linked list at that index. This allows us to store multiple values at the same index and still be able to retrieve them using their key.
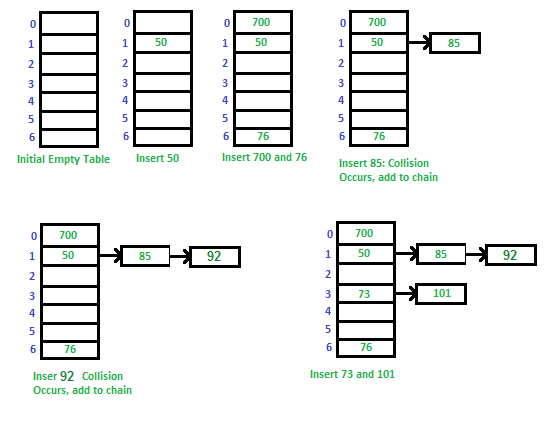
Way to implement Hash Table using Separate Chaining
Way to implement Hash Table using Separate Chaining:
Create two classes: ‘Node‘ and ‘HashTable‘.
The ‘Node‘ class will represent a node in a linked list. Each node will contain a key-value pair, as well as a pointer to the next node in the list.
Python3
class Node:
def __init__( self , key, value):
self .key = key
self .value = value
self . next = None
The ‘HashTable’ class will contain the array that will hold the linked lists, as well as methods to insert, retrieve, and delete data from the hash table.
Python3
class HashTable:
def __init__( self , capacity):
self .capacity = capacity
self .size = 0
self .table = [ None ] * capacity
The ‘__init__‘ method initializes the hash table with a given capacity. It sets the ‘capacity‘ and ‘size‘ variables and initializes the array to ‘None’.
The next method is the ‘_hash‘ method. This method takes a key and returns an index in the array where the key-value pair should be stored. We will use Python’s built-in hash function to hash the key and then use the modulo operator to get an index in the array.
Python3
def _hash( self , key):
return hash (key) % self .capacity
The ‘insert’ method will insert a key-value pair into the hash table. It takes the index where the pair should be stored using the ‘_hash‘ method. If there is no linked list at that index, it creates a new node with the key-value pair and sets it as the head of the list. If there is a linked list at that index, iterate through the list till the last node is found or the key already exists, and update the value if the key already exists. If it finds the key, it updates the value. If it doesn’t find the key, it creates a new node and adds it to the head of the list.
Python3
def insert( self , key, value):
index = self ._hash(key)
if self .table[index] is None :
self .table[index] = Node(key, value)
self .size + = 1
current = self .table[index]
while current:
if current.key = = key:
current.value = value
current = current. next
new_node = Node(key, value)
new_node. next = self .table[index]
self .table[index] = new_node
self .size + = 1
The search method retrieves the value associated with a given key. It first gets the index where the key-value pair should be stored using the _hash method. It then searches the linked list at that index for the key. If it finds the key, it returns the associated value. If it doesn’t find the key, it raises a KeyError.
Python3
def search( self , key):
index = self ._hash(key)
current = self .table[index]
while current:
if current.key = = key:
return current.value
current = current. next
raise KeyError(key)
The ‘remove’ method removes a key-value pair from the hash table. It first gets the index where the pair should be stored using the `_hash` method. It then searches the linked list at that index for the key. If it finds the key, it removes the node from the list. If it doesn’t find the key, it raises a `KeyError`.
Python3
def remove( self , key):
index = self ._hash(key)
previous = None
current = self .table[index]
while current:
if current.key = = key:
if previous:
previous. next = current. next
self .table[index] = current. next
self .size - = 1
previous = current
current = current. next
raise KeyError(key)
‘__str__’ method that returns a string representation of the hash table.
Python3
def __str__( self ):
for i in range ( self .capacity):
current = self .table[i]
while current:
elements.append((current.key, current.value))
current = current. next
return str (elements)
Here’s the complete implementation of the ‘HashTable’ class:
Python3
class Node:
def __init__( self , key, value):
self .key = key
self .value = value
self . next = None
class HashTable:
def __init__( self , capacity):
self .capacity = capacity
self .size = 0
self .table = [ None ] * capacity
def _hash( self , key):
return hash (key) % self .capacity
def insert( self , key, value):
index = self ._hash(key)
if self .table[index] is None :
self .table[index] = Node(key, value)
self .size + = 1
current = self .table[index]
while current:
if current.key = = key:
current.value = value
current = current. next
new_node = Node(key, value)
new_node. next = self .table[index]
self .table[index] = new_node
self .size + = 1
def search( self , key):
index = self ._hash(key)
current = self .table[index]
while current:
if current.key = = key:
return current.value
current = current. next
raise KeyError(key)
def remove( self , key):
index = self ._hash(key)
previous = None
current = self .table[index]
while current:
if current.key = = key:
if previous:
previous. next = current. next
self .table[index] = current. next
self .size - = 1
previous = current
current = current. next
raise KeyError(key)
def __len__( self ):
return self .size
def __contains__( self , key):
self .search(key)
return True
except KeyError:
return False
# Driver code
if __name__ = = '__main__' :
# Create a hash table with
# a capacity of 5
ht = HashTable( 5 )
# Add some key-value pairs
# to the hash table
ht.insert( "apple" , 3 )
ht.insert( "banana" , 2 )
ht.insert( "cherry" , 5 )
# Check if the hash table
# contains a key
print ( "apple" in ht) # True
print ( "durian" in ht) # False
# Get the value for a key
print (ht.search( "banana" )) # 2
# Update the value for a key
ht.insert( "banana" , 4 )
print (ht.search( "banana" )) # 4
ht.remove( "apple" )
# Check the size of the hash table
print ( len (ht)) # 3
Output
True False 2 4 3
Time Complexity and Space Complexity:
- The time complexity of the insert, search and remove methods in a hash table using separate chaining depends on the size of the hash table, the number of key-value pairs in the hash table, and the length of the linked list at each index.
- Assuming a good hash function and a uniform distribution of keys, the expected time complexity of these methods is O(1) for each operation. However, in the worst case, the time complexity can be O(n), where n is the number of key-value pairs in the hash table.
- However, it is important to choose a good hash function and an appropriate size for the hash table to minimize the likelihood of collisions and ensure good performance.
- The space complexity of a hash table using separate chaining depends on the size of the hash table and the number of key-value pairs stored in the hash table.
- The hash table itself takes O(m) space, where m is the capacity of the hash table. Each linked list node takes O(1) space, and there can be at most n nodes in the linked lists, where n is the number of key-value pairs stored in the hash table.
- Therefore, the total space complexity is O(m + n).
Conclusion:
In practice, it is important to choose an appropriate capacity for the hash table to balance the space usage and the likelihood of collisions. If the capacity is too small, the likelihood of collisions increases, which can cause performance degradation. On the other hand, if the capacity is too large, the hash table can consume more memory than necessary.



